本文并不是为初学者所编写的入门文章，而是为曾经系统学习过数据结构与算法，但发现自己走的太快，想要重新系统回顾一下的人准备的。

概述

学习数据结构 (data structure) 时，始终思考下面三点内容：

• 数据的逻辑结构 (logical structure)
• 数据的存储结构 (storage structure)
• 数据的运算 (operation)

逻辑结构

数据的逻辑结构是为我们人类所服务的。当我们在说树、图、表、堆、栈等内容时，其实指的都是逻辑结构。 逻辑结构可以看作是从具体问题中抽象出来的数学模型，它与数据的存储方式无关。 逻辑结构大体上可分为三类：

• 逻辑结构
  • 集合
  • 线性结构
  • 树形结构

存储结构

数据的存储结构是为计算机所服务的。计算机能理解的是存储结构，所以我们需要将逻辑结构映射为存储结构！ 存储结构指的就是数据在计算机中的存储方式，通常是下面四种存储方式的组合：

• 存储结构
  • 顺序存储结构 (sequential storage structure)
  • 链式存储结构 (linked storage structure)
  • 索引存储结构 (indexed storage structure)
  • 哈希存储结构 (hashed storage structure)

顺序存储结构：采用一组连续的存储单元存放所有的数据元素。 链式存储结构：每个数据元素用一个内存结点存储，每个结点是单独分配的，所有的结点地址不一定是连续的。 索引存储结构：除了存储数据元素外，还会建立一张索引表，来获取元素的存储地址。 哈希存储结构：又称散列存储结构，核心思想是是根据数据的内容，借助哈希/散列函数计算出一个值，这个值就是数据的存储地址。

运算

数据运算指的是对数据实施的操作。比如最基本的：

• 增
• 删
• 改
• 查
• 排序
• 遍历

不同的数据结构，还会有自己独特的运算，比如图的运算方式有 DFS 和 BFS

逻辑结构、存储结构和运算之间的关系

对于一种数据结构，其逻辑结构永远是唯一的，但它的存储结构可以是多种，而且在不同的存储结构中，同一种运算的实现方式也可能不同。

比如二叉树，当我们讨论二叉树时，几乎每个人在纸上画的二叉树都是差不多的，而且不管你是横着画还是竖着画，别人都是能理解的，因为我们所理解的是同一个逻辑结构。但是二叉树的具体实现却是各种各样，你可以使用顺序存储结构（比如数组），也可以使用链式存储结构（比如链表），甚至可以两个结合起来（链表的结点是数组）。而根据你的实现方式不同，你实现二叉树的运算（比如遍历等操作）时，也会不同。

这个在纸上画的方式、或者口述、或者和人交谈时你的肢体动作、或者你自己设计了一种字符串、这些都是数据结构的表示方式，而且表示的是数据的逻辑结构！

 define operation                       implement operation
       |                                         |
       |                                         |
       |                                         |
       v                  mapping                v
logical structure  -------------------->  storage structure

算法

定义：算法 (algorithm) 是对特定问题求解步骤的一种描述，它是指令的有限序列。

• 算法的 5 个重要特性：
  • 有穷性
  • 确定性
  • 可行性
  • 有输入
  • 有输出

有穷性：必须在有穷时间内结束。

确定性：对于相同输入的输入，必须有相同的输出，不能有二义性。

• 算法设计的目标
  • 正确性
  • 用户友好性
  • 可读性
  • 健壮性
  • 高效率
  • 低存储量

上面几个目标中，必须要记住的就是 健壮性。也就是要求该算法能够对不合理的数据进行检查！之所以强调这一点，而不强调其他几点，不是说其他的不重要，而是因为其他几点强调了也没啥用，因为那是能力问题。但 健壮性 不同，这是意识问题！只要你时刻记住健壮性，那么你在拿到数据时，就会先思考一下这个数据是否可以小于 0，是否可以是非数字类型。这也是为什么很多在线 IO 的答案中，即使题目明确了输入范围，但代码中仍然会判断一下数据是否在合理范围之内！

算法复杂度

• 算法复杂度
  • 时间复杂度 time complexity
  • 空间复杂度 space complexity

这里只提一下空间复杂度。一个算法的存储量包括三个方面：

• 输入数据所占空间
• 程序本身所占空间
• 临时变量所占空间

在分析算法的空间复杂度时，通常只考虑临时变量所占空间。注意函数形参不计入临时变量。

线性表

linear list

常见的存储结构：

• 顺序存储结构 —— 顺序表 (sequential list)
• 链式存储结构 —— 链表 (linked list)

线性表的基本运算：

• 创建（申请空间）
• 初始化（值）
• 销毁（释放空间）
• 获取长度
• 判断是否为空表
• 打印输出
• 获取第 i 个数据元素值
• 查找某个数据元素
• 插入数据元素到指定位置
• 删除数据元素
• 排序

常见的逻辑结构（通常是使用链式存储结构）：

• 单链表
• 双链表
• 循环链表

链表相关术语：

• 头指针 (head pointer)
• 首指针 (first pointer)
• 尾指针 (tail pointer)

通常每个链表都带有一个头结点，头指针就指向头结点。而链表的第一个数据元素是在首结点中，首指针就指向首结点。

当然，这说的是通常情况，如果你要自己实现一个头结点和首结点是同一个结点的链表，也可以！

栈

栈 (stack) 是一种操作受到限制的线性表。它最重要的特性就是 后进先出 (LIFO, Last In First Out)。

常用存储结构为

• 顺序存储结构
• 链式存储结构

相关术语：

• 栈顶 (top)
• 栈底 (bottom)
• 进栈 (push)
• 出栈 (pop)

栈的基本运算

• 初始化（空栈）
• 销毁（释放空间）
• 判断栈是否为空
• 进栈
• 出栈
• 获取栈顶元素（不出栈）

队列

队列 (queue) 也是一种操作受到限制的线性表。它最重要的特性就是 先进先出 (FIFO, First In First Out)。

常用存储结构（思考一下如何使用两个栈实现队列）

• 顺序存储结构
• 链式存储结构

基本运算

• 初始化（空队列）
• 销毁（释放空间）
• 判断队列是否为空
• 入队（插入队尾）
• 出队

常见逻辑结构类型：

• 队列
• 循环队列
• 双端队列

相关术语：

• 队尾 (rear)
• 队首 (front)
• 入队 (enqueue)
• 出队 (dequeue)
• 假溢出 (false overflow)

假溢出：在循环队列中，由于判断队列是否已满的条件设置不合理而导致队列已满，但实际上还有空位置。

串

串 (string) 是由零个或多个字符组成的有限序列。

串的存储结构通常为顺序存储结构。当然，你也可以使用链式存储结构。

基本运算

• 生成串
• 销毁串
• 复制串
• 判断串是否相等
• 获取串的长度
• 拼接串
• 提取子串
• 插入子串
• 删除子串
• 替换子串
• 输出串

相关术语：

• 空串
• 子串 (substring)
• 子序列 (subsequence)

子串指的是串中一段任意长度的 连续 字符所组成的序列。

子序列指的是从串中按顺序提取出的任意长度的可 非连续 字符所组成的序列。

常见算法

• BF (Brute-Force) 暴力算法
• KMP 算法

KMP 指的是三位大佬：D. E. Knuth、J. H. Morris 和 V. R. Pratt。

字符串的存储方式

如果你使用过 c 语言，那么你应该和发现 c 语言中不存在“字符串”，其他语言所提供的字符串，其实是它内部帮你实现了“字符串”这一数据结构。所以这里可以进一步讨论一下串的存储方式。一般来说，一个字节（8 位）可以表示一个字符（假设只存储 ASCII 码）。而计算机内存是 按字编址，即以‘字’作为存储单位，一个存储单位就是一个‘字’大小。而一个‘字’具体表示多少个字节，则取决与机器。比如 64 位操作系统上，一个‘字’通常是 64 位（8 个字节）。

那么， 这个时候使用顺序存储串时，你就可以有多种选择了：是选择一个‘字’存储一个字符，还是选择一个‘字’存储多个字符（即一个字节存储一个字符）呢？很明显，前者的占用空间大，但处理起来方便，比如 c 语言你可以直接使用 char 来存储一个 ASCII 字符。而后者的占用空间小，但处理起来很麻烦，比如 c 语言中你需要使用 char char / unsigned char 来存储一个 ASCII 字符。

之所以在这里提及这个，是因为很多“神奇”的算法都涉及到这种思维，比如各种使用位运算的神奇操作。

计算机架构中，一个 word (字) 被定义一个指定位长的数据单位，当计算机处理器和内存直接进行寻址时，就会用到这个数据单位。专业点说，word 代表的是计算机中数据总线的宽度。通常，一个 word 的长度会是 8 的倍数，因为一个字节通常是 8 位。¹

递归

数组

数组太过常见了，常见到我不知道应该如何来介绍它。因为不同编程语言中有对于的数组，对于没有学过 c 语言的人，或者只学习过 js 语言的人来说，可能在看到线性表和数组这两个内容居然分开讲时，就已经蒙圈了。

在 c 语言中，数组一旦指定大小，就不能改变了，如果非要改变，就得重新申请新的空间，然后复制过去。而在 js 语言中，基本不需要考虑这种情况。但考虑到申请的空间，需要重新申请空间，这一需求在算法设计中算是常见的，所以这里指的数组是永远较多限制的数组结构。

数组的基本运算：

• 初始化
• 销毁
• 读操作
• 写操作

由于数组使用非常频繁，所以各种高级语言中都有很多有关数组的 api，这些 api 都可以尝试自己实现一下。

数组涉及的相关术语，主要是和矩阵相关：

• 按行优先存储
• 按列优先存储
• 对称矩阵 (Symmetric matrix)
• 上三角矩阵 (upper triangular matrix)
• 下三角矩阵 (lower triangular matrix)
• 对角矩阵 (diagonal matrix)
• 稀疏矩阵 (sparse matrix)
• 三元组表 (list of 3-tuples)

对称矩阵：矩阵内元素满足 a_ij = a_ji

上三角矩阵和下三角矩阵，是根据主对角线（对角线指的是方向是 \）进行划分的。上三角矩阵指的是矩阵的左下 (◣) 部分的所有元素均为常数。下三角矩阵指的是右上 (◥) 部分的所有元素是常量。

对角矩阵，类似与上三角矩阵和下三角矩阵的组合，要求主对角线的上面和下面都有相同条非零元素构成的次对角线。

稀疏矩阵：当矩阵中的非零元素非常少时，就称为稀疏矩阵。这种时候，如果还用二维数组来存储就有点浪费空间了。我们可以用三元组 (i, j, a_ij) 来表示这些非零元素。

广义表

广义表 (generalized) 是线性表的推广，就像多位数组是一维数组的推广一样。广义表中的元素数量是任意的，元素的类型可以是原子类型（不可再分隔的数据类型，也可以是另一个广义表。js 中的数组其实就相当于广义表。

广义表的存储结构通常是链式存储，因为很难为一个广义表分配固定大小的存储空间。

基本运算：

• 创建
• 销毁
• 求广义表的长度
• 求广义表的深度
• 打印输出

树

树的常见逻辑表示方法

• 树形表示法 (tree representation)
• 括号表示法 (bracket representation)
• 文氏图表示法 (venn diagram representation)
• 凹入表示法 (concave representation)

树的遍历:

• 先根遍历 (preOrder transversal)
• 后根遍历 (postOrder transversal)
• 层次遍历 (level transversal)

常见术语

• 结点的度 (degree of node)
• 树的度 (degree of tree)
• m 次树 (m-tree)
• 分支结点 (branch node)
• 叶子结点 (leaf node)
• 路径 (path)
• 路径长度 (path length)
• 子结点 (child node)
• 父结点 (parent node)
• 兄弟结点 (sibling)
• 子孙结点 (descendant)
• 祖先结点 (ancestor)
• 结点层次 (level)
• 结点深度 (depth)
• 树的高度 (height)
• 树的深度 (depth)
• 有序树 (ordered tree)
• 无序树 (unordered tree)
• 森林 (forest)

结点的度：结点的子树个数

树的度：树的所有结点中，最大的结点的度

m 次树：度为 m 的树

分支结点：度不为 0 的结点

路径：一个结点序列

路径的长度：路径上的分支的数量（即结点序列 - 1）

有序树：树中的每个结点的子树都是按照一定次序从左到右安排的，且相对次序是不能随意改变的。无特别说明时，树指的都是有序树。

二叉树

二叉树 (binary tree) 是严格区分左右子树的。

基本分类：

• 满二叉树 (full binary tree)
• 完全二叉树 (complete binary tree)

常见存储结构：

• 顺序存储结构
• 链式存储结构

基本运算

• 构造二叉树
• 销毁（释放空间）
• 查找特定结点
• 获取左子结点
• 获取右子结点
• 获取高度
• 先序遍历 (preOrder transversal)
• 中序遍历 (inOrder transversal)
• 后序遍历 (postOrder transversal)
• 层序遍历 (level transversal)
• 以括号表示法打印输出（序列化）

线索二叉树

相关术语：

• 前驱结点 (predecessor node)
• 后驱结点 (successor node)
• 线索二叉树 (threaded binary tree)

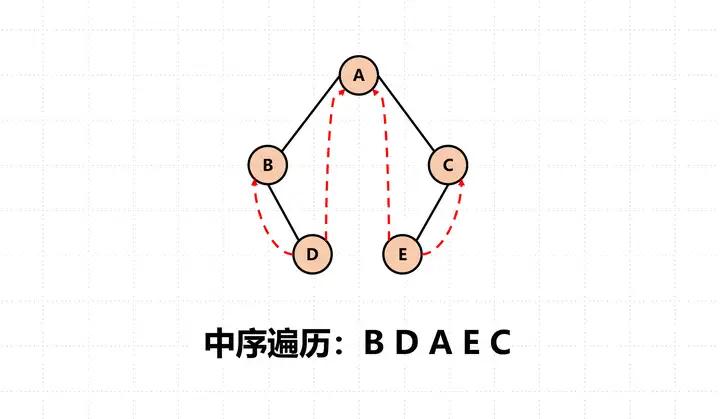
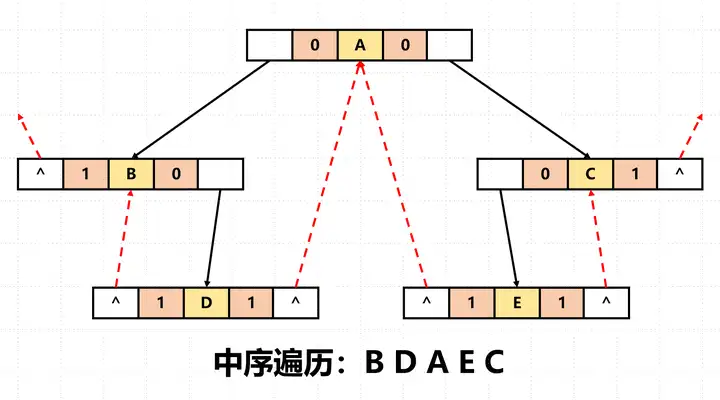
先序/中序/后续遍历过程中，一个结点的前驱结点指的就是遍历当前结点前所在结点；一个结点的后驱结点就是遍历当前结点后所在结点。

当某个结点的左指针为空时，让其指向该结点的前驱结点；

当每个结点的右指针为空时，让其指向该结点的后驱结点；

线索二叉树指的通常是中序遍历中的前驱结点和后驱结点。

哈夫曼树

相关术语：

• 权 (weight)
• 带权路径长度 (WPL, Weighted Path Length)
• 哈夫曼树 (Huffman tree)

权：结点所携带的有意义的数值。

带权路径长度：根结点到当前结点之间的路径长度和该结点上的权的乘积。

哈夫曼树：，又称最优二叉树，表示带权路径长度最小的二叉树。

相关算法：

• 构造哈夫曼树
• 哈夫曼编码

构造哈夫曼的算法很简单：每次从还未被选取的结点中，选取两个数值最小的结点，然后合成一个新结点。重复此步骤，直到所有结点都被选取过。

哈夫曼编码：将需要编码的字符作为结点，其权值等于该字符在电文中出现的次数，然后构造出哈夫曼树。规定哈夫曼树的左分支为 0，右分支为 1。那么各个字符所到根结点的路径，就是该字符的编码。

并查集

图

常见存储方式有：

• 邻接矩阵 (adjacency matrix)
• 邻接表 (adjacency list)

图的基本运算：

• 创建
• 销毁
• 遍历
• 打印输出

常见算法：

• 深度优先遍历 (DFS, Depth First Search)
• 广度优先遍历 (BFS, Breadth First Search)

生成树和最小生成树

一个连通图的极小连通子图就是 生成树 。所以生成树中的边的数量一定等于顶点数量 - 1。也就是说生成树中不会存在环，或者说如果在生成树上再添加任意一条边，那么就一定会出现一个环。

如果连通图中的每条边都有权值，那么所有生成树中，权值之和最小的就是 最小生成树。

常见算法：

• 普里姆算法 (Prim)
• 克鲁斯卡尔算法 (Kruskal)

最短路径

常见算法

• Dijkstra 算法
• 弗洛伊德算法 (Floyd)

拓扑排序

有向图 V 中的顶点序列 v1,v2, ..., vn 如果满足：若 vi 到 vj 有路径，则 vi 在 vj 的前面。那么这个序列就称为拓扑序列。

在有向图中寻找一个拓扑序列的过程称为拓扑排序 (topological sort)

AOE 网

相关术语：

• 源点 (source)
• 汇点 (converge)
• 关键路径 (critical path)
• 关键活动 (key activity)
• AOE 网 (activity on edge network)

用一个有向无环图描述工程的预计进度，顶点表示事件，有向边表示活动，边的权表示完成活动所需要的时间，或者说活动持续时间。入度为 0 的顶点表示开始事件（开工），出度为 0 的点表示结束事件（完工），这样的一个带权的有向无环图称为 AOE 网。

源点：入度为 0 的顶点，也就是开始事件（开工）

汇点：出度为 0 的顶点，也就是结束事件（完工）

关键路径：AOE 网中，从源点到汇点的所有路径中，路径长度最大的路径

关键活动：关键路径上的顶点

查找算法

常见算法

• 顺序查找 (sequential search)
• 折半查找 (binary search)
• 分块查找 (block search)

相关术语

• 动态查找表 (dynamic search table)
• 静态查找表 (static search table)
• 内查找 (internal search)
• 外查找 (external search)
• 平均查找长度 (ASL, Average Search Length)
• 比较树 (comparison tree) / 判定树 (decision tree)

动态查找表：查找的同时进行增删改操作

静态查找表：查找时不涉及增删改操作

内查找：整个查过过程都只在内存中

外查找：查找过程中需要访问外存

判定树/比较树：折半查找的过程可以使用二叉树表示，把当前查找区间的中间位置上的元素作为二叉树的根，根的左子树是左子表所构成的二叉树，右子树同理。

二叉搜索树

二叉搜索树 (BST, binary search tree) 又称二叉排序树。重要性质： BST 的中序遍历结果是一个递增有序序列

基本运算

• 创建
• 插入
• 查找
• 删除

平衡二叉树

平衡二叉树通常指的是 AVL 树。平衡二叉树在 BST 的基础上增加了树形的约束，即每个结点都是平衡的。

基本运算

• LL 型调整
• RR 型调整
• LR 型调整
• RL 型调整
• 创建
• 插入
• 查找
• 删除

B_ 树

外查找

B+ 树

外查找

哈希表查找

常见术语：

• 哈希表 (hash address)
• 哈希函数 (hash function)
• 哈希地址 (hash address)
• 哈希冲突 (hash collisions)
• 同义词 (synonym)
• 装填因子 (load factor)

哈希函数构造方法

• 直接定址法
• 除留余数法
• 数字分析法

哈希冲突解决方案

• 线性探测法 (linear probing)
• 平方探测法 (square probing)
• 拉链法 (chaining)

排序

内排序

• 插入排序
  • 直接插入排序
  • 折半插入排序
  • 希尔排序 / 分组插入排序
• 交换排序
  • 冒泡排序
  • 快速排序
• 选择排序
  • 简单选择排序
  • 堆排序
• 归并排序
• 基数排序

外排序

• 磁盘排序
• 磁带排序

生成初始归并段 多路平衡归并 最佳归并树